Neurogéométrie et contours subjectifs
Notre travail propose un résumé de l’approche dite neurogéométrique des contours illusoires (où l’on perçoit des bords en l’absence de contours dans l’image réelle) et plus généralement de la perception visuelle des formes en introduisant les concepts de géométrie algébrique qui permettent de saisir dans un cadre mathématique rigoureux cette classe de phénomènes tout en trouvant un ancrage dans l’organisation fonctionnelle du cortex extrastrié. On conclura en proposant d’autres liens que pourrait entretenir ce formalisme algébrique avec les propriétés du système visuel.
Les contours illusoires
Largement
étudiés par un des piliers de la Gestalttheorie, Gaetano Kanizsa[1],
les contours subjectifs[2] -- dont le parangon
est sans doute le triangle éponyme (fig. ci-contre) -- devinrent l’objet de controverses[3] que l’on peut résumer dans l’opposition entre
les tenants d’une explication bottom-up (i.e. un traitement bas-niveau du
système visuel) et les défenseurs d’une reconstruction top-down (qui voit
là l’oeuvre des aires supérieures complétant une forme pour la faire correspondre
à un prototype a priori). Le débat, loin de s’apaiser
est incessamment renouvelé par les données psychophysiques[4] et neurobiologiques[5] d’une part, mais aussi par la mise en place de
modèles plus précis qu’ils soient computationnels (de type connexionnistes,
par exemple) et/ou mathématiques qui semblent favoriser les hypothèses ascendantes.
L’organisation fonctionnelle du cortex visuel
Il
est important pour la compréhension de l’exposé de rappeler quelques données
élémentaires concernant l’organisation des aires primaire (V1 ou aire 17)
et secondaire (V2, 18). Les neurones de ces aires ont la spécificité de répondre
par une décharge de potentiels d’action lorsque l’on présente une barre orientée
suivant un angle spécifique dans une zone donnée du champ visuel (dite « champ
récepteur » du neurone considéré). En effet, l’une des grandes découvertes
des neurosciences fut la démonstration frappante (par Hubel & Wiesel,
en 1959 puis par Tootell et al.[6], cf. Fig. ci-contre)
de l’organisation rétinotopique des aires visuelles primaires : sur la
surface du cortex est reproduite à une transformation géométrique près, la
carte de la rétine.
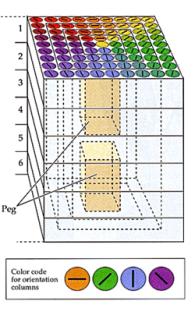Auparavant,
à une échelle plus fine, Hubel et Wiesel[7]
avaient pu démontrer l’organisation en colonnes d’orientation des cortex striés
et extrastriés. Sur la figure ci-dessus, on peut voir une représentation de
ces organisations fonctionnelles : Une cible projetée sur un écran entraîne
un patron d’activation homologue sur le cortex visuel. Sur le schéma on a
indiqué l’orientation préférentielle des neurones pour une zone donnée du
champ visuel ; en chaque point du champ sensoriel est associé l’une de ces
colonnes, dont les cellules ont des champs récepteurs qui se recouvrent mais
des orientations préférentielles distinctes et ordonnées comme indiqué sur
le schéma. On pourra parler de « goniotopie ».
Pour cet exposé, nous nous limiterons à ces éléments fonctionnels, faisant abstraction des questions de la perception de la couleur, du mouvement,... mais aussi des problèmes de dominance oculaire. Malgré ces restrictions, nous allons étudier le cas des contours illusoires : en effet, lorsque l’on présente une figure du type « Triangle de Kanizsa » les neurones ne devraient pas décharger puisque la surface est uniformément blanche, pourtant, indéniablement, nous percevons une forme ! La question est alors de savoir où émerge ce percept dans le système visuel.
La géométrie de V1
Une inspiration relativement récente dans le champ des neurosciences vient de la géométrie algébrique : comment représenter mathématiquement la structure fonctionnelle du cortex visuel et rendre compte de ses propriétés ? Si le patron de connectivité des neurones visuels s’identifie à une topologie (les connexions représentant un « voisinage »), les propriétés de ces connexions définissent une métrique : un neurone sera d’autant plus proche d’un autre qu’il lui sera « fortement » connecté, on pourra alors dire que la distance entre ces deux est d’autant plus courte.
On
peut alors interpréter la transmission de l’information dans le cortex visuel
comme une propagation de l’information sur la métrique du réseau neuronal.
En observant que les neurones situés dans le prolongement des amorces (les
bords formés par les cercles découpés) sont activés par diffusion de l’activité
de proche en proche (ce résultat est dû à Peterhans et van der Heydt), une
hypothèse élémentaire pour l’explication du phénomène de complétion modale
consisterait donc à imaginer que les bords anomaux qui apparaissent dans les
figures de type Kanizsa sont en fait des plus courts chemins dans l’espace
géométrique : entre deux points, les neurones activés seraient ceux
situés sur la ligne droite joignant ces deux points. Ce faisant, on introduit
l’idée que cette métrique est uniforme : le signal se propage par diffusion
atténuée. Ce modèle ne permet toutefois pas de rendre compte du fait que
la diffusion est aussi nette que le percept car par diffusion simple (c’est-à-dire
sur une métrique euclidienne) on observerait une activité comme sur la figure
3 : le centre se voit effectivement occupé par une forme triangulaire plus
claire, mais les contours sont relativement flous.
Cette modélisation ne tient pas compte d’une propriété essentielle de V1 qui est son organisation fonctionnelle. Pour ce faire, il faut prendre en compte le fait que les neurones avec des orientations préférentielles colinéaires sont connectés entre eux (cf. Gilbert, 1992[8]). Pour être plus précis, ce patron de connectivité est tel que la géométrie de l’espace visuel se caractérise par une double propriété de distance (la rétinotopie) et de tangence (la « goniotopie »). La structure rétinotopique peut s’expliciter au moyen d’une projection, toutefois cette opération est plus délicate qu’il n’y paraît : les neurones (qu’ils soient simples ou complexes) échantillonnent le champ visuel avec un certain degré de granularité mais surtout au travers de filtres dits de Gabor qui garantissent la spécificité d’orientation de chacun d’entre eux. Or, comme on l’a observé, l’ordonnancement des neurones sur cette « goniotopie » dépend de leur orientation préférentielle, si bien qu’en chaque point de l’espace visuel M*, de coordonnées (x,y), le système visuel fait correspondre une colonne d’orientation -- en réalité, un point de l’espace visuel est de la taille d’un champ récepteur. Le formalisme des fibrations permet de traiter le cas de telles applications surjectives tout en garantissant des résultats puissants de géométrie différentielle au niveau local. On voit donc l’intérêt d’introduire une telle structure dans notre modèle du système visuel. (Pour plus de détails mathématiques, nous renvoyons à Tondut, 1997[9] et Petitot & Tondut, 1999[10])
Un problème variationnel dans l’espace de fibré contact
Outre l’organisation géographique des neurones, le cortex visuel est caractérisé par le patron de connectivité qui met en contact les neurones les uns avec les autres. Or les observations d’abaissement de seuil de détectabilité4 de facilitation électrophysiologique[11] ou de marquage de connections cortico-corticales8 confirment le fait que les neurones sont organisés de façon à favoriser la détection de segments alignés, voire à compléter d’éventuels contours manquants.
Dans l’étude des contours illusoires cette donnée se révèle
d’une grande importance : En conservant, une approche variationnelle
du problème, nous obtenons là une contrainte supplémentaire sur le chemin
que doit suivre le signal dans l’organisation corticale : le chemin minimal
doit suivre une courbe tangente à l’orientation préférentielle des neurones
en chacun de ses points. Il est alors possible de formuler le problème de
la détermination de cette activité neuronale
collective
comme la minimisation du chemin sur une relevée legendrienne de la courbe
rétinotopique du contour. Pour cet exposé, on pourra se contenter de savoir
que la relevé legendrienne d’une courbe F en deux dimensions y=f(x) est la
courbe G définie dans l’espace à 3 dimensions par
le triplet 
.
Si l’approche variationnelle n’est pas inédite dans la
modélisation de la vision[12], la nouveauté de
l’emploi de techniques de minimisation sur un fibré de contact réside dans
la plus grande pertinence biologique du modèle car sans cette contrainte de
tangence, il faut introduire une hypothèse a priori dans le problème qui est
sinon sous-contraint[13]. La méthode la plus
courante consiste à minimiser la courbure le long du chemin rétinotopique,
i.e. le long de l’abscisse curviligne tout en gardant le chemin aussi court
que possible. Il s’agit d’une minimisation de l’énergie de courbure avec une
contrainte sur l’abscisse curviligne de chemin : 
; le
contour étant défini par
F = {(x,y) / (y=f(x), xÎ[xa,xb])
et f(xa)=ya, f(xb)=yb} où les
points (xa, ya) et (xb,yb) définissent
les deux amorces de la courbe.
Dans l’espace fibré, la minimisation fait intervenir le
lagrangien : L=
Dans cet opérateur
les termes dans le plan de l’espace de base (la carte rétinotopique) constituent
la contribution à la minimisation du chemin (l
dans la minimisation précédente) et le terme différentiel correspond à celle
de la relevée legendrienne.
David Mumford a introduit une classe de fonctions baptisées Elasticae[14] qui se trouvent être des solutions pour l’équation en courbure dans le plan de base. Or ces fonctions si elles peuvent être obtenues au sein d’équations différentielles relativement accessibles, ne peuvent être utilisées aussi efficacement dans les problèmes variationnels. A l’inverse, la formulation différentielle des solutions des géodésiques legendriennes dans le fibré de contact est inexploitable. Toutefois, en associant simplifications et/ou approximations numériques (nécessaires du fait même de la discrétisation de l’échantillonnage de l’image par le système visuel), on peut obtenir des données numériques qu’il est possible de confronter à l’expérimentation.
Face à l’expérience
Les données expérimentales semblent confirmer les modèles proposés pour la complétion de contours en formulation variationnelle. Toutefois, il n’existe pas (à notre connaissance) de paradigmes expérimentaux assez fins permettant de départager ces différents modèles sur la base de leurs prédictions. On peut malgré cela, noter que le modèle neurogéométrique s’inscrit dans un cadre plus cohérent avec les données actuelles de la neurobiologie fonctionnelle du système visuel. Forts des progrès de l’IRM de diffusion dans le traçage des connexions nerveuses[15] (avec une précision infra-millimétrique), il nous sera peut-être bientôt possible de valider le concept de relevée legendrienne sur des bases purement neuroanatomiques...
D’autre
part, on a pu observer une convergence assez remarquable de cette interprétation
avec les modèles psychophysiques de Field[16] et coll.
(cf. fig. ci dessus) malgré la pauvreté des données quantitatives des modèles
psychophysiques. On peut aussi noter que la non-linéarité du processus perceptif
s’intègre parfaitement dans le cadre de notre modèle : R. Shapley[17] et coll.
mentionne ainsi l’exemple des contours subjectifs avec inversion de phase
(voir figure ci-contre). Pour rendre compte de la continuité du contour
malgré des amorces en opposition de phase (en termes de filtres de Gabor)
il est nécessaire d’avoir des termes non-linéaires d’ordre pair dans la formulation
énergétique ce qui est effectivement le cas dans ce modèle.
Une remarque plus fondamentale qui peut être faite à cette approche porte sur l’absence des processus dynamiques : cette critique porte d’autant plus que d’autres auteurs (Gray[18] et plus récemment, T. S. Lee[19], par exemple) font des synchronies locales le mécanisme fondamental mis en oeuvre durant les tâches d’intégration, de contours en particulier. Mais, et c’est là l’une des forces de cette approche, il n’est pas exclu d’introduire un terme temporel dans la fonctionnelle géodésique pour tenir compte de ces effets dynamiques. D’autant plus que l’on pourrait envisager d’abandonne la simplification qui a été faite du cercle S1 en la droite projective P1 afin de mieux rendre compte des expériences de « pop-out » sur les contours fermés. De même, face aux critiques d’auteurs comme P. Tse[20], qui favorise une approche en terme de complétion de volume, on peut imaginer de projeter l’espace de base sur une fibre vectorielle où la profondeur serait aussi encodée. Cette perspective d’étendre l’espace 1-jet (un paramètre d’orientation par colonne) à un espace n-jets pour rendre compte d’une multiplicité de propriété des surfaces de l’espace visuel (le « 2½D Sketch » de D. Marr[21]) : orientation mais aussi profondeur (les hypercolonnes font intervenir la disparité binoculaire, négligée jusqu’alors) voire tangence de surface. On obtiendrait alors une formulation non plus en terme de chemin minimal mais en surfaces minimales ce qui nous rapprocherait encore des données les plus récentes sur la perception des contours illusoires comme frontières de surfaces subjectives[22]. Enfin, si les obstacles mathématiques ne l’interdisent pas, il est envisageable d’étendre cette approche à d’autres mécanismes sensoriels voire plus proprement cognitifs.
Karim N’Diaye – Fev. 2002
